In an electronic world, digital signatures are used to sign documents. This signing process is performed by applying an encryption algorithm to the document. This article will generally touch on symmetric and asymmetric encryption processes, how the private and public keys are used in this system, and hash functions.

Digital signatures are used in lots of different places nowadays. For example, they are used in various areas like electronic bills and electronic rulers.

In this article, I'll give examples for the blockchain side, but the general structure is valid in all systems.

Encryption and Hash Functions

Although hashing and encryption sound like the same thing, they are completely different from each other.

With encryption, your inputs can be rendered unreadable with certain algorithms and solvent keys; if you have a solvent key, you can decrypt your inputs.

With hashing, your inputs can be rendered unreadable; however, since hash functions are a one-way operation, even if the hash value is captured, it is almost impossible to restore the input to its previous state with today's computers.

Lots of hash functions (SHA1, MD5, SHA256, etc.) are used. SHA256 is the most popular and is used in the blockchain. SHA-256 is a hash algorithm standardized by the NIST (National Institute of Standards and Technology) and is used in various applications. SHA256 creates a 256-bit hash for every input.

If we change only a bit of character in this example, you will see that the output has completely changed. Let's substitute a dot for the exclamation marks and see what happens.

We will use this algorithm frequently for the purpose of verifying the immutability of the transmitted data. Now that we have hashed our message, how are we going to convey it to the other side?

Symmetric Encryption

These subjects are already quite complex and confusing. Thus, I believe it is appropriate to provide a short explanation and utilize graphical samples. For the remaining headings, we shall, in brief, use Alice, Bob, and their cheerful friends.

At a table with seating for 10, Alice and Bob are trying to communicate with one another. However, nobody should be able to see their messages. How can Alice and Bob accomplish that?

Alice puts her message in the box and locks it. Then she gives the key and box to Bob. And yay! We did it. The remaining 8 people don't know Alice's message anymore. Only Alice and Bob can read the message. No one can't see what's inside without the key, so Alice attentively should send the key to Bob. We don't want the key stolen, right?

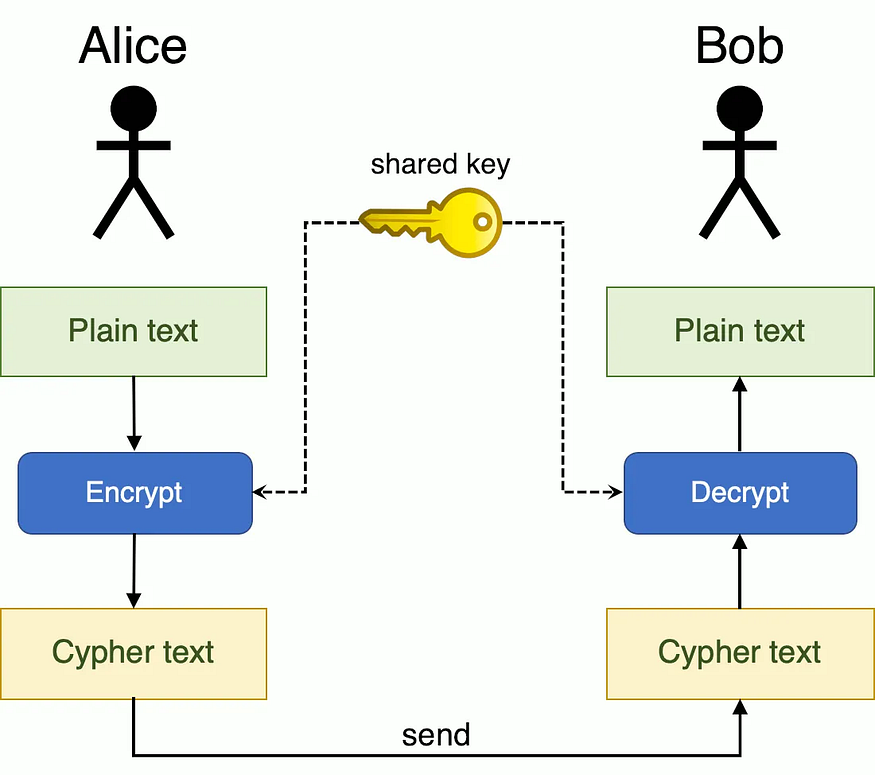
This key represents our private key. Alice has a key and a box; anybody can't read the message because the box is locked. Alice's only purpose is to get the private key safely to Bob. The problem is starting at this point. You can consider options such as sending by mail or writing on paper, but unfortunately, none of these is sustainable or practical.

Although symmetric encryption has created a revolution, the use of public keys leads to major security vulnerabilities. But still, symmetric encryption was used for many years, until someone came up with an extraordinary idea.

Asymmetric Encryption

Whitfield Diffie suggested a new idea in 1976. What if, contrary to all thought, we shared our key?

A secure encryption key exchange between two parties is described by the Diffie-Hellman key exchange protocol. With this protocol, users may safely display their keys even if they don't trust one another. Using safe encryption, one may utilize this approach to communicate data between two users.

Now, let's integrate Alice and Bob and examine the system step by step.

It's the same situation again: Alice has a message to send to Bob, and this message has to be sent safely.

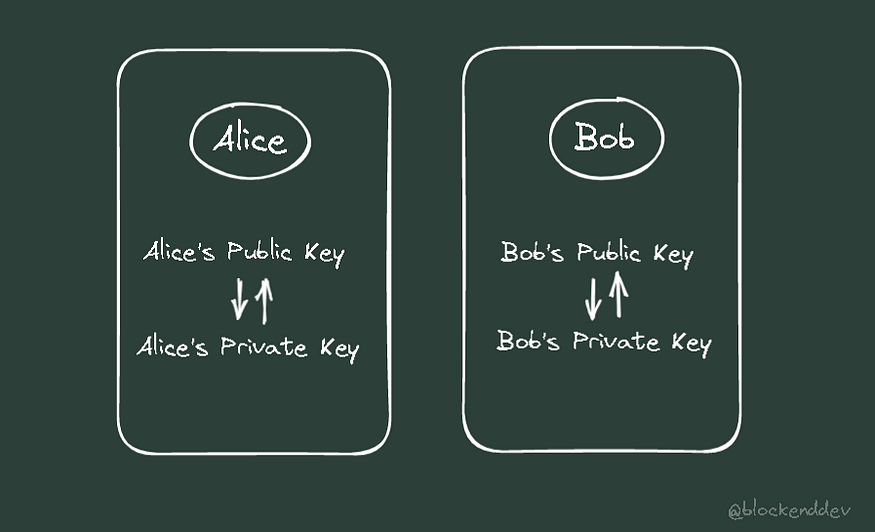
Both Alice and Bob have key pairs that are connected to and compatible with one another, but only one of them is public and the other is private.

Because these key pairs are connected, the message that was encoded by one of them may be unlocked by the other.

Now let's use these key pairs to communicate our message.

1. After Alice writes the message she wants to send to Bob, she uses her private key to encrypt the message. So, this message only can be decrypted with Alice's public key.

2. Alice, hash the encrypted message with the SHA256 hash function.

3. Alice uses Bob's public key to sign hashed message. In this way, it is verified that the message was read by Bob.

4. Alice send encrypted, hashed, and signed message to Bob.

5. Bob gets the message and uses his own private key to open signed message. In this way, since the message had been encrypted with its own public key, Bob decrypt the message easily.

6. After Bob decrypted the message, Bob verify signature of the message with Alice's public key to verify message had send really by Alice. If the signature of the message is verified, Bob makes sure that the message was sent by Alice and reads the message.

In this approach, a message is safely transferred between Alice and Bob, and transactions are read using cryptographic signature techniques. These techniques provide for the safe signing of transactions while also allowing for the verification of the validity of those transactions.

Let's try to answer some of the questions that could remain in people's minds regarding the sixth step (the verification step).

Q1: Bob achieve to arrive hashed message but he see only hash in his hands. How can he read Alice's “I love you” message when he only has the hashed message in his hand?

(Hash functions are a one-way operation, even if the hash value is captured, it is almost impossible to restore the input to its previous state)

Bob will never understand Alice's feelings for him, despite the fact that she sent him a "I love you" message. Even if it's terrible, it's real. Sending both a signed and encrypted message as well as an unencrypted message is the best course of action if Alice truly wants to express her love for him (directly, "I love you").

Only in this way can Bob learn. First, he uses Alice's public key to encrypt the "I love you" message before hashing it. The message is correct if the hashes match; otherwise, it is wrong. as hashing operations are one-way and never return results.

In addition, there is also one more way for Bob to understand Alice's feelings for him. Alice could say her encrypted message in just two steps. Step 1: Encrypt the message with Bob's public key and send it to Bob. Step 2: Bob decrypts the message with his private key and accesses the message (directly, "I love you").

Actually, this is the most basic form of asymmetric encryption. But of course, it contains compromises from the immutability of the data, and that the message really came from Alice.

Q2: Okey, I got it. But what is the purpose of encryption the message after we send the message directly? We could have already sent it at first.

Each user connects his wallet to a dapp and makes some web3 transactions. If you connect your wallet to the NFT marketplace, this can be transactions such as buying NFT or making an offer. When we make transactions on the Web3 website, we make a lot of signing transactions. Accordingly, we send the messages we have signed to the other party. Even if we send a message to the other side, we don't want it to be read in such areas. But if we need proof, we can take the data and prove it. Alice also said: "Look, I told you I loved you," which is proof, as she might say.

Q3: Can't everybody do the verification process when Alice send the message directly? Because everyone can able to access Alice's public key.

Nope, only Alice and Bob's message has been hashed. In short, only Alice and Bob can verify.

Asymmetric encryption aka public key encryption provides mutual use of the public key, not the private key. If you want to create a wallet on a chain such as Ethereum or Solana, you will have 256-bit public and private keys. So, how are these compatible public and private keys generated?

RSA and Elliptic Curve Algorithm (ECDSA)

There are numerous algorithms used for public key encryption. We'll keep an eye out for the two most well-known algorithms, RSA and the Elliptic Curve Algorithm. Let's examine how to create a key without diving deep into cryptography.

RSA (Rivest-Shamir-Adleman) cryptography algorithm is used to encrypt data safely and decrypt messages. RSA was developed by Ron Rivest, Adi Shamir and Leonard Adleman in 1978 and is still used in lots of projects.

The following example demonstrates how the RSA algorithm works:

1. First, two prime numbers are selected and these numbers are named as p and q. For example, p=5 and q=13 can be selected.

2. Then, the number n which is the product of p and q is calculated. n is used as the public key. n=pq, so n=5.13=65.

3. Using the function known as the Euler function (φ(n)), the number (phi) that remains from the product of p and q is calculated. phi=(p-1)(q-1), so phi=(5–1)(13–1)=48.

4. Next, a number e is selected and this number should be between 1 and phi. For example, e=17 can be selected. e is used as the public key.

5. Finally, the number d is calculated by applying modulo operation between e and phi. For example, d=27 is calculated. d is used as the private key.

6. As a result of these operations, a pair of public key (n=65, e=17) and private key (n=65, d=27) is created. These keys are used for securely encrypting data and performing decryption operations.

For more information about RSA Algorithm

---

The elliptic curve digital signature algorithm (ECDSA) is a cryptography algorithm, and this algorithm is used for verify verifying of messages or data.

If a user wants to send a message or data to other users, he encrypts the message or data and sends the encrypted message or data to other users. If this message or data is verified and verified by the user to whom it was sent, it is verified that the message or data was actually sent by the user to whom it was sent.

ECDSA performs this verification process and, afterward, creates a digital signature. This digital signature verifies the authenticity of the message or data and at the same time ensures that this change can be detected if the message or data has not been modified or changed. With this method, the accuracy of the message or data and the non-modification are ensured.

The ECDSA is demonstrated in the following example:

1. Firstly, an elliptic curve is selected. This curve is a mathematical structure with various features and is used in cryptography systems.

2. Next, a point is selected on this curve, referred to as G and its coordinates, (x, y), are expressed.

3. Then, a private key is chosen and referred to as d. d is a number and must have a value between 0 and (n-1). After that, the Q point, referred to as the public key, is calculated using the G point and the d private key value.

4. Q point has (x, y) coordinates and these coordinates are used as the public key.

5. As a result of these processes, the (x, y) and d as the private key pairs are generated. These keys are used for securely encrypting data and performing decryption operations.

We have selected elliptic curve and private and public keys, now let's do a signing operation:

1. A communication is established between Alice and Bob, and Alice informs Bob that she wants to send a message.

2. Then, using the ECDSA algorithm, the public key and private key pairs are generated between Alice and Bob.

3. Alice sends Bob the public key pair she will use to encrypt the message.

4. Bob encrypts the message using the received public key pair and sends the encrypted message to Alice.

5. Alice uses her private key pair to decrypt the received encrypted message and obtains the original message.

For more information about Elliptic Curve Algorithm

---

Cryptography is an infinite ocean. Therefore, even a little bit of knowledge will help us. Of course, at first you may not fully understand RSA and ECDSA. If you don't interest in cryptography, it's enough to know fundamental information. So, if it's not your area of interest, please focus on the fundamental spaces.

As you know, Alice and Bob have 256-bit public and private keys. I just want to make a point that I think attentive readers can take. We have to answer all the questions, right?

Q4: For example, the key that I share with people in my wallet on Ethereum, which I link to my wallet, consists of only 40 characters. How is this happening?

First off, on Ethereum, expressions that begin with 0x are really our account number rather than our public or private key. It is shorter than public and private keys, and it is not problematic for us to share the same public key with others or even to create a Twitter account.

Q5: We have never used our ens domains (wallet addresses) for encryption and signing transactions, why was this needed? Wasn't the public key enough?

The public key and private key are used in asymmetric encryption, and they are connected to one another. You can encrypt a message with the public key and use the private key to decode the encrypted message. Between the sender and the receiver of the message, a secure channel of communication is formed in this way. They have already been discussed in great depth above.

After creating an account on the Ethereum network, your wallet address is connected to a public key and used for doing transactions on the network. Your wallet address is a special address you use to identify yourself when transacting on the Ethereum network. This address is also used to validate your transactions. Without your wallet address, you are unable to conduct transactions on the Ethereum network or create an account. Since transactions on the Ethereum network need having your wallet address, having it is crucial for the Ethereum network.

Conclusion

Our whole goal was to whisper in Alice's ear that she loved Bob. We learned hash functions, we created our public and private keys with the help of RSA and ECDSA, and we learned signing operations. In short, we have passed many stages, if you have come so far without getting bored, without giving up, congratulations.

You have touched on an important topic that Blockchain 101-102 topics are passed superficially, which is generally ignored and not considered in the learning process of courses and training.

---

Do not hesitate to send a message for questions or criticisms that are stuck in your mind. You can follow the author on his social media accounts:

• Twitter: https://twitter.com/blockenddev

• Blog: https://emreaslan.hashnode.dev

• Github: https://github.com/emreaslan7